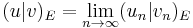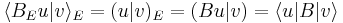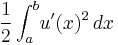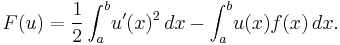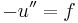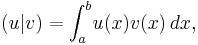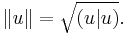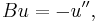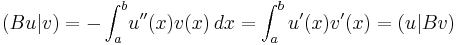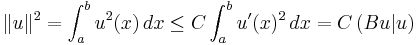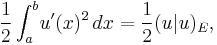Energetic space
In mathematics, more precisely in functional analysis, an energetic space is, intuitively, a subspace of a given real Hilbert space equipped with a new "energetic" inner product. The motivation for the name comes from physics, as in many physical problems the energy of a system can be expressed in terms of the energetic inner product. An example of this will be given later in the article.
Contents |
Energetic space
Formally, consider a real Hilbert space  with the inner product
with the inner product 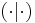 and the norm
and the norm  . Let
. Let  be a linear subspace of
be a linear subspace of  and
and 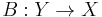 be a strongly monotone symmetric linear operator, that is, a linear operator satisfying
be a strongly monotone symmetric linear operator, that is, a linear operator satisfying
 for all
for all 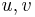 in
in 
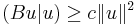 for some constant
for some constant 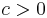 and all
and all  in
in 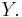
The energetic inner product is defined as
 for all
for all 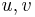 in
in 
and the energetic norm is
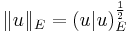 for all
for all  in
in 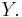
The set  together with the energetic inner product is a pre-Hilbert space. The energetic space
together with the energetic inner product is a pre-Hilbert space. The energetic space 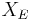 is defined as the completion of
is defined as the completion of  in the energetic norm.
in the energetic norm. 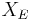 can be considered a subset of the original Hilbert space
can be considered a subset of the original Hilbert space 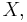 since any Cauchy sequence in the energetic norm is also Cauchy in the norm of
since any Cauchy sequence in the energetic norm is also Cauchy in the norm of  (this follows from the strong monotonicity property of
(this follows from the strong monotonicity property of  ).
).
The energetic inner product is extended from  to
to 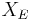 by
by
where 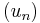 and
and 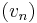 are sequences in Y that converge to points in
are sequences in Y that converge to points in 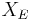 in the energetic norm.
in the energetic norm.
Energetic extension
The operator  admits an energetic extension
admits an energetic extension 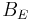
defined on 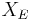 with values in the dual space
with values in the dual space 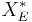 that is given by the formula
that is given by the formula
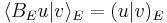 for all
for all 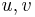 in
in 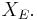
Here, 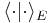 denotes the duality bracket between
denotes the duality bracket between 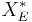 and
and 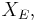 so
so 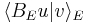 actually denotes
actually denotes 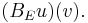
If  and
and  are elements in the original subspace
are elements in the original subspace 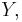 then
then
by the definition of the energetic inner product. If one views 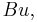 which is an element in
which is an element in 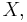 as an element in the dual
as an element in the dual 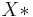 via the Riesz representation theorem, then
via the Riesz representation theorem, then 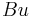 will also be in the dual
will also be in the dual 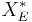 (by the strong monotonicity property of
(by the strong monotonicity property of  ). Via these identifications, it follows from the above formula that
). Via these identifications, it follows from the above formula that 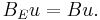 In different words, the original operator
In different words, the original operator 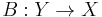 can be viewed as an operator
can be viewed as an operator 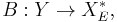 and then
and then 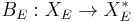 is simply the function extension of
is simply the function extension of  from
from  to
to 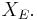
An example from physics
Consider a string whose endpoints are fixed at two points 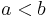 on the real line (here viewed as a horizontal line). Let the vertical outer force density at each point
on the real line (here viewed as a horizontal line). Let the vertical outer force density at each point 
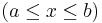 on the string be
on the string be 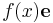 , where
, where 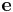 is a unit vector pointing vertically and
is a unit vector pointing vertically and ![f:[a, b]\to \mathbb R.](/2012-wikipedia_en_all_nopic_01_2012/I/6a75b1184ddade1d85dd3cc2914d9ccd.png) Let
Let 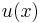 be the deflection of the string at the point
be the deflection of the string at the point  under the influence of the force. Assuming that the deflection is small, the elastic energy of the string is
under the influence of the force. Assuming that the deflection is small, the elastic energy of the string is
and the total potential energy of the string is
The deflection 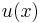 minimizing the potential energy will satisfy the differential equation
minimizing the potential energy will satisfy the differential equation
with boundary conditions
To study this equation, consider the space 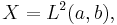 that is, the Lp space of all square integrable functions
that is, the Lp space of all square integrable functions ![u:[a, b]\to \mathbb R](/2012-wikipedia_en_all_nopic_01_2012/I/dc309d98144038a5a19f3c0f60eabbd0.png) in respect to the Lebesgue measure. This space is Hilbert in respect to the inner product
in respect to the Lebesgue measure. This space is Hilbert in respect to the inner product
with the norm being given by
Let  be the set of all twice continuously differentiable functions
be the set of all twice continuously differentiable functions ![u:[a, b]\to \mathbb R](/2012-wikipedia_en_all_nopic_01_2012/I/dc309d98144038a5a19f3c0f60eabbd0.png) with the boundary conditionss
with the boundary conditionss 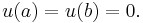 Then
Then  is a linear subspace of
is a linear subspace of 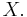
Consider the operator 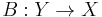 given by the formula
given by the formula
so the deflection satisfies the equation 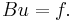 Using integration by parts and the boundary conditions, one can see that
Using integration by parts and the boundary conditions, one can see that
for any  and
and  in
in 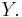 Therefore,
Therefore,  is a symmetric linear operator.
is a symmetric linear operator.
 is also strongly monotone, since, by the Friedrichs' inequality
is also strongly monotone, since, by the Friedrichs' inequality
for some 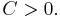
The energetic space in respect to the operator  is then the Sobolev space
is then the Sobolev space 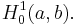 We see that the elastic energy of the string which motivated this study is
We see that the elastic energy of the string which motivated this study is
so it is half of the energetic inner product of  with itself.
with itself.
To calculate the deflection  minimizing the total potential energy
minimizing the total potential energy 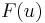 of the string, one writes this problem in the form
of the string, one writes this problem in the form
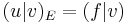 for all
for all  in
in 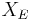 .
.
Next, one usually approximates  by some
by some 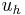 , a function in a finite-dimensional subspace of the true solution space. For example, one might let
, a function in a finite-dimensional subspace of the true solution space. For example, one might let 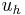 be a continuous piecewise-linear function in the energetic space, which gives the finite element method. The approximation
be a continuous piecewise-linear function in the energetic space, which gives the finite element method. The approximation 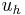 can be computed by solving a linear system of equations.
can be computed by solving a linear system of equations.
The energetic norm turns out to be the natural norm in which to measure the error between  and
and 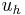 , see Céa's lemma.
, see Céa's lemma.
See also
References
- Zeidler, Eberhard (1995). Applied functional analysis: applications to mathematical physics. New York: Springer-Verlag. ISBN 0387944427.
- Johnson, Claes (1987). Numerical solution of partial differential equations by the finite element method. Cambridge University Press. ISBN 0521345146.